DEFINICIÓN
a y N son dos números reales positivos (a ≠1 ),
Para aclarar el concepto, podríamos decir que logaritmo es solo otra forma de expresar la
potenciación, como en este ejemplo:
Que leeremos: logaritmo de 9 en base 3 es igual a 2
Esto significa que una potencia se puede expresar
como logaritmo y un logaritmo se puede expresar como potencia.
El gráfico siguiente nos muestra el nombre que
recibe cada uno de los elementos de una potencia al expresarla como logaritmo:
Entonces, podemos
preguntar: ¿Que es el logaritmo?
El logaritmo es "el exponente" al cual se debe elevar la base para obtener
la potencia.
Ejemplos: Aplicando la
definición de logaritmo
1)
El resultado (2) es el exponente por el cual debemos elevar la base (2) para obtener la potencia (4): 22 = 4
2)
El resultado (0) es el exponente por el cual debemos elevar la base (2) para obtener la potencia (1): 20 = 1
3)
El resultado (y) es el exponente por el cual
debemos elevar la base (1/2) para obtener la potencia (0,25):
Pero en este
caso debemos despejar el exponente y:
4)
5)
Cuidado con esto, hay que recordarlo: Cuando la
base no aparece expresada se supone que ésta es 10:  el 10
que indica la base, no se coloca, se supone, así:
el 10
que indica la base, no se coloca, se supone, así:
7)
Con lo ya expuesto, podemos empezar a establecer
las:
PROPIEDADES DE LOS LOGARITMOS
No
existe el logaritmo de un número con base negativa.
No
existe el logaritmo de un número negativo.
No
existe el logaritmo de cero.
El
logaritmo de 1 es cero.
El
logaritmo en base a de a es uno.
El
logaritmo en base a de una potencia en base a es igual al exponente.
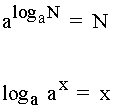
1) Si los logaritmos de dos números son iguales, los números también son iguales:
2) El logaritmo de un producto es igual a la suma de los logaritmos de
los factores:
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
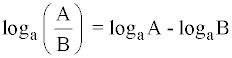
El logaritmo de una potencia es igual
al producto del exponente por el logaritmo de la base:
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
Cambio de base:
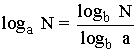
LOGARITMOS DECIMALES Y NEPERIANOS
Logaritmos
decimales:
Son los que tienen base 10. Se representan por
log (x) (ya vimos que la base 10 no se escribe, queda implícita).
Logaritmos
neperianos o naturales:
Son los que tienen base e. Se representan por
ln (x) o L(x) (ya vimos que la base e tampoco se escribe, se subentiende
cuando aparece ln).
Algunos ejemplos de logaritmos neperianos son:
ln 1 = 0; puesto que e0 = 1
ln e2 = 2; puesto que e2 = e2
ln e−1 = −1; puesto que e−1 = e−1
El número e
tiene gran importancia en las Matemáticas. No es racional (no es cociente de
dos números enteros) y su valor, con seis cifras decimales, es
e = 2,718281...
EJEMPLOS
Aquí, otra nota importante, para no olvidar: Los
logaritmos que tienen base e se
llaman logaritmos neperianos o
naturales. Para representarlos se escribe ln o bien L. La
base e está implícita, no se
escribe:
EJERCICIOS RESUELTOS
I) Calcula los siguientes logaritmos:
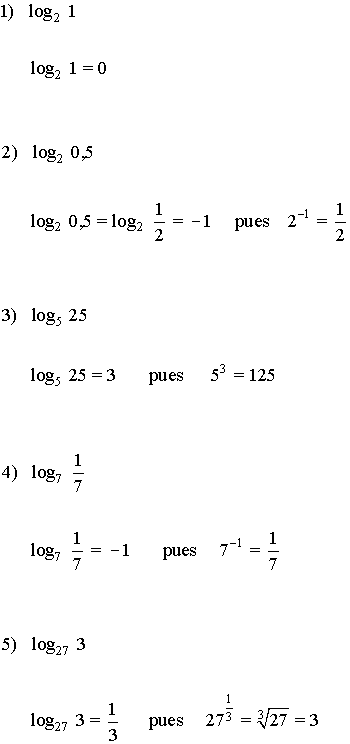
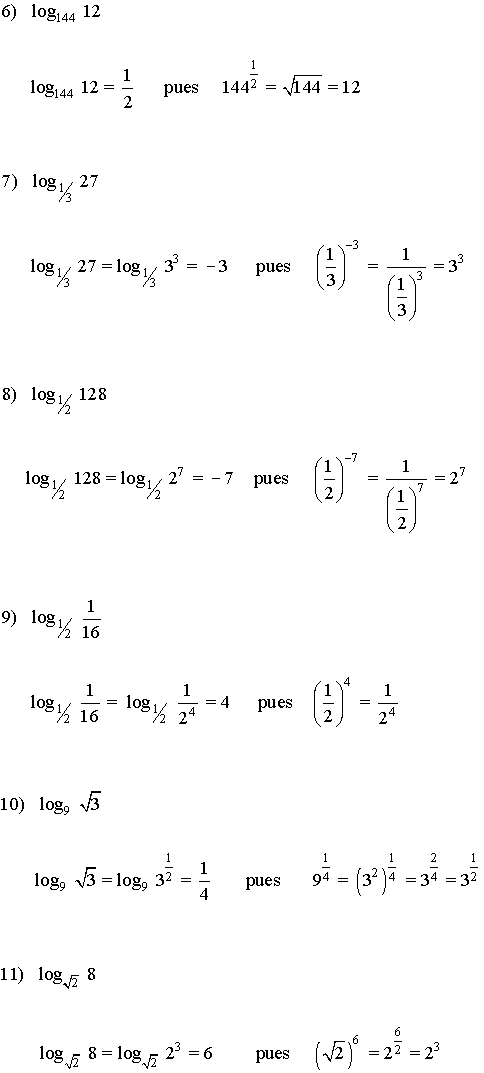
II) Calcula los siguientes logaritmos en base 10:
5a) Calcula aplicando las propiedades de los logaritmos:
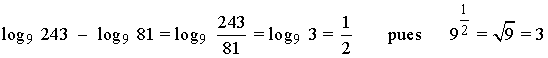
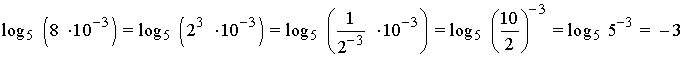
III) Calcula los siguientes logaritmos sabiendo que: log 2 = 0,301030 , log 3 = 0,477121


IV) Calcula los siguientes logaritmos cambiándolos a base decimal:
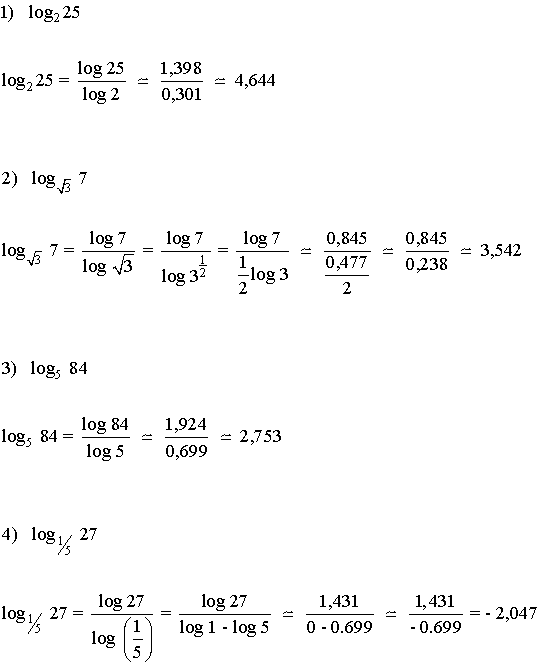
V) Calcula:
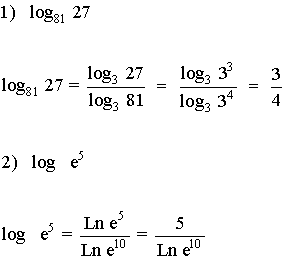
No hay comentarios:
Publicar un comentario