NÚMEROS IMAGINARIOS

Definición

Un número imaginario se denota por bi, donde:

b es un número real

i es la unidad imaginaria

Unidad imaginaria La unidad imaginaria es el número  y se designa por la letra i. La "unidad" imaginaria (el equivalente al 1 de los números reales) es √(-1) (la raíz cuadrada de menos uno). En matemáticas se usa i (de imaginario) pero en electrónica se usa j (porque "i" ya es la corriente, y la letra siguiente después de la i es la j). Un número que cuando se eleva al cuadrado (se multiplica por sí mismo) da un resultado negativo. Pero imagina que hay un número (vamos a llamarlo i de imaginario) que cumpliera esto: i × i = -1 ¿Sería útil, qué podríamos hacer con él? Bueno, haciendo la raíz cuadrada de los dos lados tendríamos un valor para la raíz cuadrada de -1: Y eso es muy útil... simplemente aceptando que exista i podemos resolver muchos problemas donde nos hace falta la raíz cuadrada de un número negativo. Ejemplo: ¿cuál es la raíz cuadrada de -9? Respuesta: √(-9) = √(9 × -1) = √(9) × √(-1) = 3 × √(-1) = 3i Mientras tengamos esa pequeña "i" ahí para recordarnos que hay que multiplicar por √-1 no tendremos problemas con seguir calculando para llegar a la solución.

Ejemplos de números imaginarios

i

12.38i

-i

3i/4

0.01i

-i/2

Los números imaginarios no son "imaginarios"

De hecho hubo un tiempo en que se pensó que los números imaginarios eran imposibles, y por eso se llamaban "imaginarios" (a modo de broma).

Pero después hubo gente que investigó más y descubrió que son útiles e importantes porque rellenan un hueco en matemáticas... pero el nombre de "imaginario" se mantuvo.

Utilidad

Aquí tienes dos ejemplos en los que son útiles:

Electricidad

		La CA o AC (corriente alterna) cambia de positivo a negativo siguiendo una onda sinuoidal. Si combinas dos corrientes alternas puede que no coincidan bien, y puede ser muy difícil calcular la nueva corriente. Pero usar números reales e imaginarios juntos hace mucho más fáciles los cálculos.
		Y el resultado puede ser corriente "imaginaria", ¡pero puede hacerte daño igual!

Ecuación cuadrática

	Una ecuación cuadrática puede dar resultados con números imaginarios...
... pero quizás después de más cálculos el número "i" se cancela (o se convierte en real porque está al cuadrado), dando una respuesta que es real.

Propiedad interesante

La unidad imaginaria, i, tiene una propiedad interesante. "Da la vuelta" pasando por 4 valores diferentes cuando la multiplicas:

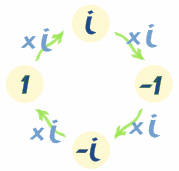
So, i × i = -1, ... después -1 × i = -i, ... después -i × i = 1, ... después 1 × i = i (¡de vuelta i!)

Conclusión

La unidad imaginaria, i, es igual a la raíz cuadrada de menos 1 (-1) Los números imaginarios no son "imaginarios", son de verdad y son útiles, ¡y puedes tener que usarlos algún día!