DEFINICIÓN.
Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas que cumplen ciertas reglas fijas, cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación.
Cuadrado de la suma de dos cantidades o binomio cuadrado
(a + b)2 = a2 + 2ab + b2 |
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
Demostración:
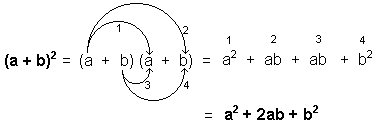
Cuadrado de la diferencia de dos cantidades
(a − b)2 = a2 − 2ab + b2 |
El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
Demostración:
Producto de la suma por la diferencia de dos cantidades
(o producto de dos binomios conjugados)
(a + b) (a – b) = a2 – b2 |
El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el cuadrado de la segunda
Demostración:
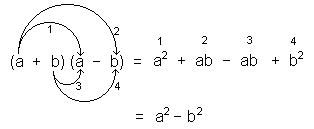
Producto de dos binomios con un término común, de la forma:
(x + a) (x + b) = x2 + (a + b)x + ab |
(x + a) (x – b) = x2 + (a – b)x – ab |
Demostración:
x2 – (a + b)x + ab = (x – a) (x – b) |
Demostración:
(mx + a) (nx + b) = mnx2 + (mb + na)x + ab |
En este caso, vemos que el término común (x) tiene distinto coeficiente en cada binomio (mx y nx).
Demostración:
Cubo de una suma de dos cantidades
(a + b)3 = a3 + 3a2b + 3ab2 + b3 |
(a – b)3 = a3 – 3a2b + 3ab2 – b3 |
Trinomio al cuadrado
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc |
A modo de resumen, se entrega el siguiente cuadro con Productos notables y la expresión algebraica que lo representa:
Producto notable | Expresión algebraica | Nombre | |
(a + b)2
|
=
|
a2 + 2ab + b2
|
Binomio al cuadrado
|
(a + b)3
|
=
|
a3 + 3a2b + 3ab2 + b3
|
Binomio al cubo
|
a2 - b2
|
=
|
(a + b) (a - b)
|
Diferencia de cuadrados
|
a3 - b3
|
=
|
(a - b) (a2 + b2 + ab)
|
Diferencia de cubos
|
a3 + b3
|
=
|
(a + b) (a2 + b2 - ab)
|
Suma de cubos
|
a4 - b4
|
=
|
(a + b) (a - b) (a2 + b2)
|
Diferencia cuarta
|
(a + b + c)2
|
=
|
a2 + b2 + c2 + 2ab + 2ac + 2bc
|
Trinomio al cuadrado
|
No hay comentarios:
Publicar un comentario