Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente. Como por ejemplo:
Propiedades de las ecuaciones exponenciales:
1) La función exponencial es siempre positiva:
2) Si dos potencias de la misma base son iguales, los exponentes son iguales:
3) Si x e y son números
reales y a y b son números reales positivos, entonces se
verifican las siguientes igualdades:
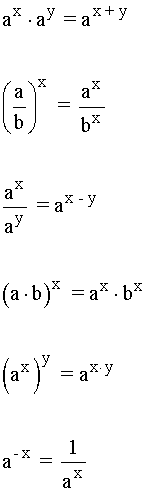
Resolver las siguientes ecuaciones exponenciales:
1) 2x = 8
Ecuación: 2x = 8
Factorizando: 2x = 23
Igualando: x = 3
2) 2x = 64
Ecuación: 2x = 64
Factorizando: 2x = 26
Igualando: x = 6
3) 3x = 9
Ecuación: 3x = 9
Factorizando: 3x = 32
Igualando: x = 2
4) 3x+1 = 81
Ecuación: 3x+1 = 81
Factorizando: 3x+1 = 34
Igualando: x + 1 = 4
Resolviendo: x = 3
5) 5x = 3125
Ecuación: 5x = 3125
Factorizando: 5x = 55
Igualando: x = 5
6) 2x = 22
Ecuación: log(2x) = log(22)
Despejando: x·log(2) = log(22)
Resolviendo: x = log(22) / log(2)
x = 4,46
Resolver las siguientes ecuaciones exponenciales:
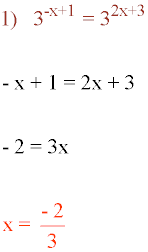
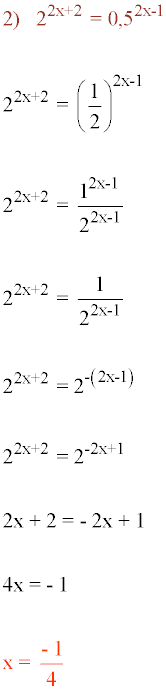
Resolver las siguientes ecuaciones exponenciales:
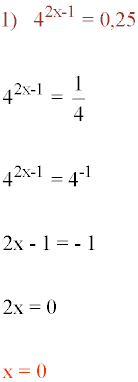
Resolver las siguientes ecuaciones exponenciales:
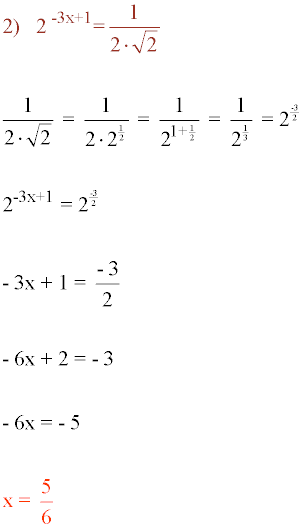
Resolver la siguiente ecuación exponencial:
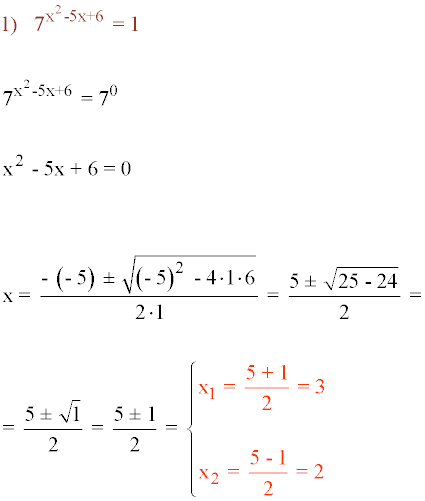
Resolver las siguientes ecuaciones exponenciales:
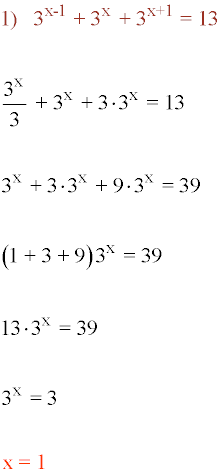
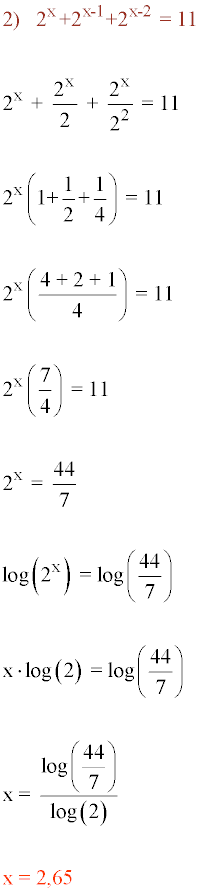
Resolver la siguiente ecuación exponencial:
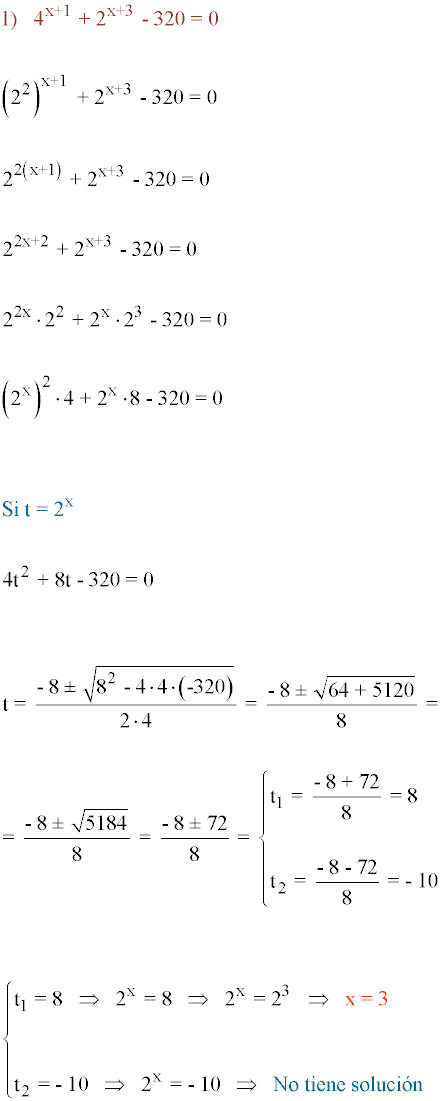
Resolver la siguiente ecuación exponencial:

Resolver la siguiente ecuación exponencial:
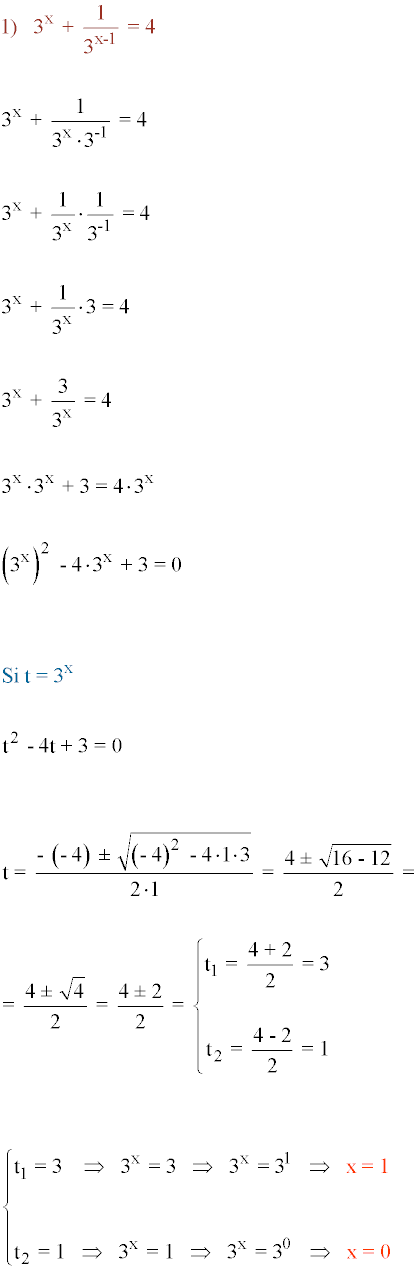
Resolver la siguiente ecuación exponencial:
EN RESUMEN
Podemos agrupar la resolución de ecuaciones exponenciales en tres casos:
A) Ambos miembros se pueden poner como potencia de la misma base
1) 5x = 25
El segundo miembro se puede expresar en la misma base que el primer miembro.5x = 52
x = 2
2) 3x - 1 + 3x + 3x + 1 = 117
Sacamos factor común: 3x (3- 1 + 1 + 3) = 117Simplificamos:
Resolvemos: 3x = 27 = 33 ⇒ x = 3
B) Se reduce a una ecuación de segundo grado
1) 52x - 30 · 5x + 125 = 0
Operamos: (5x)2 - 30 · 5x + 125 = 0
Hacemos la sustitución y = 5x : y2 - 30 · y + 125 = 0
Resolvemos la ecuación de segundo grado:
Se deshace el cambio: y = 5x = 5 ⇒ x = 1
y = 5x = 25 = 52 ⇒ x = 2
C) Cuando las ecuaciones exponenciales tienen distinta base, se pueden aplicar logaritmos
1) 3x = 8
Aplicando la definición de logaritmo tenemos que:x = log38
A continuación cambiamos a base decimal:
2) 7x - 1 - 2x + 5 = 0
Despejamos uno de los sumandos: 7x - 1 = 2x + 5
Aplicamos logaritmo a ambos miembros: log (7x - 1) = log (2x + 5)
Aplicamos la propiedad del logaritmo de una potencia: (x - 1)log 7 = (x + 5)log 2
Operamos y despejamos la incógnita x:
x log 7 - log 7 = x log 2 + 5 log 2
x log 7 - x log 2 = 5 log 2 + log 7
x (log 7 - log 2) = 5 log 2 + log 7
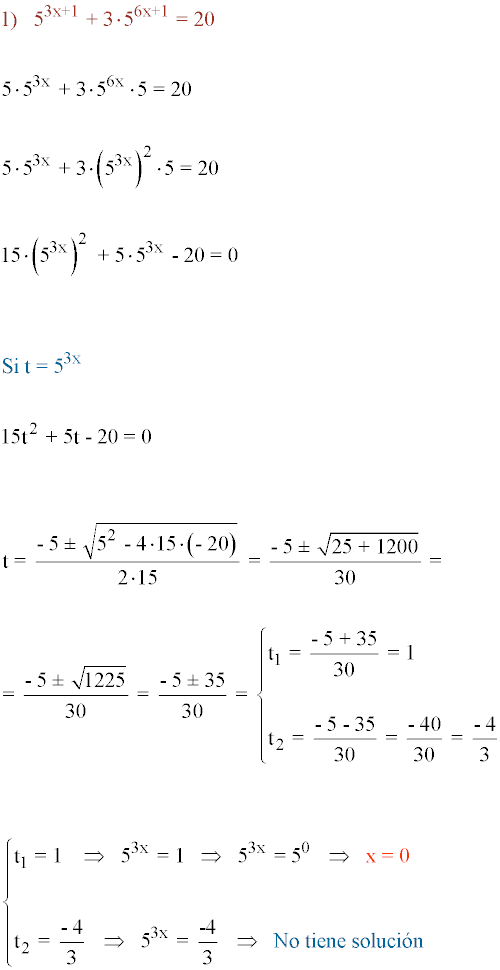
Ejercicios de ecuaciones exponenciales
ResponderEliminar