En matemáticas, se llama número racional a todo número que puede representarse como el cociente de dos números enteros o, más precisamente, un entero y un natural positivo,1 es decir, una fracción común a/b con numerador a y denominador b distinto de cero. El conjunto de los números racionales se denota por Q (o bien
, en negrita de pizarra) que deriva de «cociente». Este conjunto de números incluye a los números enteros (
), y es un subconjunto de los números reales (
).Los números racionales se representan en la recta junto a los números enteros.
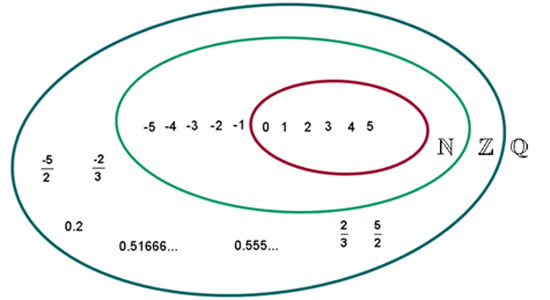
En conclusión un número racional es un número que se puede escribir en forma de fracción (o sea, como un cociente).
Por ejemplo 1,5 es un número racional porque 1,5 = 3/2 (se puede escribir en forma de fracción)
Aquí tienes más ejemplos:
| Número | En fracción | ¿Racional? |
|---|---|---|
| 5 | 5/1 | Sí |
| 1,75 | 7/4 | Sí |
| .001 | 1/1000 | Sí |
| 0,111... | 1/9 | Sí |
| √2 (raíz cuadrada de 2) | ? | ¡NO! |
¡Vaya! La raíz cuadrada de 2 no se puede escribir en forma de fracción! Y hay muchos más números así, como no son racionales se llaman irracionales.
Más ejemplos:
| p | q | Número racional |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 0,5 |
| 55 | 100 | 0,55 |
| 1 | 1000 | 0,001 |
| 253 | 10 | 2,53 |
| 7 | 0 | ¡No! ¡ "q" no puede ser cero! |
El estudiante de Pitágoras
El antiguo matemático griego Pitágoras creía que todos los números son racionales (se pueden escribir en forma de fracción), pero uno de sus estudiantes, Hipaso, demostró que no se puede escribir la raíz de 2 en forma de fracción (se cree que usando geometría) y que es por lo tanto irracional.
Pero Pitágoras no podía aceptar que existieran números irracionales, porque creía que todos los números tienen valores perfectos. Como no pudo demostrar que los "números irracionales" de Hipaso no existían, ¡tiraron a Hipaso por la borda y se ahogó!
No hay comentarios:
Publicar un comentario